√ Fisika: Mencari Nilai Variansi dan Aproksimasi Linear Menggunakan Ms.Excel

Fisika: Mencari Nilai Variansi dan Aproksimasi Linear Menggunakan Ms.Excel

Pengetahuan

Teknisi Serba Bisa

11/22/2020

Halo Sobat Teknisi, semoga semua dalam kondisi baik-baik saja.

Variansi masuk ke dalam materi pengukuran berulang untuk mengetahui nilai ketidak pastian.

Variansi σ didefinisikan sebagai berikut

Contoh mencari variansi menggunakan Microsoft Excel

Disediakan data sebagai berikut:

Pengukuran No.	xi
1	69
2	71
3	76
4	77
5	79
6	83
7	84
8	90
9	93
10	94
11	93

Cara pengerjaan

#1 Jumlahkan terlebih dahulu semua data menggunakan rumus =SUM, atau bisa juga langsung cari nilai rata-rata dari seluruh data.

Pengukuran No.	xi
1	69
2	71
3	76
4	77
5	79
6	83
7	84
8	90
9	93
10	94
11	93
Jumlah	909

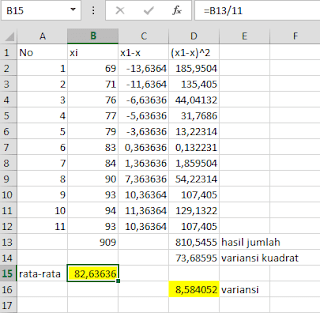
#2 cari nilai rata-rata dari 11 data di atas menggunakan jumlah data yang sudah dijumlahkan lalu dibagi 11 (total data yang ada).

#2 cari rata-rata dari data yang disajikan

#3 nilai data (xi) dikurangi dengan rata-rata

Pengukuran No.	xi	xi-(x)
1	69	-13,63636364
2	71	-11,63636364
3	76	-6,636363636
4	77	-5,636363636
5	79	-3,636363636
6	83	0,363636364
7	84	1,363636364
8	90	7,363636364
9	93	10,36363636
10	94	11,36363636
11	93	10,36363636

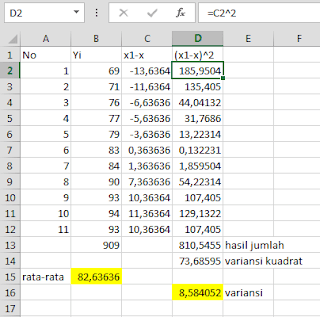
#4 setelah itu hasilnya xi-x dipangkatkan dua

Pengukuran No.	xi	x1-x	(x1-x)^2
1	69	-13,63636364	185,9504132
2	71	-11,63636364	135,4049587
3	76	-6,636363636	44,04132231
4	77	-5,636363636	31,76859504
5	79	-3,636363636	13,2231405
6	83	0,363636364	0,132231405
7	84	1,363636364	1,859504132
8	90	7,363636364	54,2231405
9	93	10,36363636	107,4049587
10	94	11,36363636	129,1322314
11	93	10,36363636	107,4049587

#5 Jumlahkan semua hasil dari (xi-x)^2 menggunakan rumus =SUM, atau bisa langsung dicari nilai rata-ratanya.

Pengukuran No.	xi	x1-x	(x1-x)^2
1	69	-13,63636364	185,9504132
2	71	-11,63636364	135,4049587
3	76	-6,636363636	44,04132231
4	77	-5,636363636	31,76859504
5	79	-3,636363636	13,2231405
6	83	0,363636364	0,132231405
7	84	1,363636364	1,859504132
8	90	7,363636364	54,2231405
9	93	10,36363636	107,4049587
10	94	11,36363636	129,1322314
11	93	10,36363636	107,4049587
Hasil Jumlah			810,5454545

#6 variansi kuadrat merupakan rata-rata dari data (xi-x)^2

Pengukuran No.	xi	x1-x	(x1-x)^2
1	69	-13,63636364	185,9504132
2	71	-11,63636364	135,4049587
3	76	-6,636363636	44,04132231
4	77	-5,636363636	31,76859504
5	79	-3,636363636	13,2231405
6	83	0,363636364	0,132231405
7	84	1,363636364	1,859504132
8	90	7,363636364	54,2231405
9	93	10,36363636	107,4049587
10	94	11,36363636	129,1322314
11	93	10,36363636	107,4049587
Hasil Jumlah			810,5454545
Variansi Kuadrat			73,68595041

#6 variansi kuadrat merupakan rata-rata dari (xi-x)^2

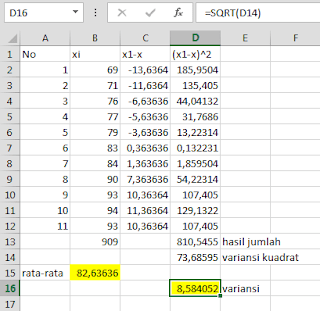
#7 karena data masih bernilai kuadrat maka kita harus mencari akarnya, barulah ketemu nilai variansi menggunakan rumus =SQRT

#7 nilai variansi akar dari variansi kuadrat

Mencari Aproksimasi Linear Menggunakan Microsoft Excel

Pengukuran besaran Y pada berbagai nilai x memberikan data bahwa Y berubah secara liner terhadap X. Ini berarti persamaan yang mengaitkan Y dengan X adalah Y = a + bX.

Contoh: Disajikan data sebagai berikut

x	y
100	138
110	142
120	152
130	154
140	158
150	166
160	168
170	180
180	186
190	188
200	186

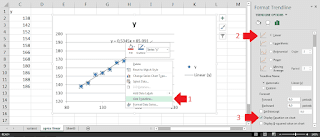
#1 Drag semua data, lalu klik insert setelah itu cari scatter atau lebih jelasnya lihat gambar di bawah ini

Kita bisa menentukan nilai dari sumbu x dan y caranya letakkan kursor pada daerah nilai sumbu x atau y yang ingin diatur nilainya setelah itu klik kanan. lalu pilih format axis

Bagaimana cara kita melihat persamaannya?

#2 klik kanan pada bullets yang ada di scatter lalu pilih add trendline

Saya kira itu temen-temen yang bisa disampaikan pada artikel kali ini. Jangan lupa untuk mengklik tombol share supaya teman yang lain juga dapat mengetahui apa yang kita ketahui, semoga bermanfaat.

Teknisi Serba Bisa